David Appell - Physics World, tháng 10/2011Những lỗ đen lang thang bị tống cổ ra khỏi hang ổ thiên hà của chúng là một trong những dự đoán bất ngờ nêu ra bởi những nhà vật lí sử dụng những cỗ máy vi tính mạnh để giải các phương trình Einstein của thuyết tương đối tổng quát. David Appell trình bày về cái mà một số người đã đặt tên là “thời đại vàng son mới” của thuyết tương đối.
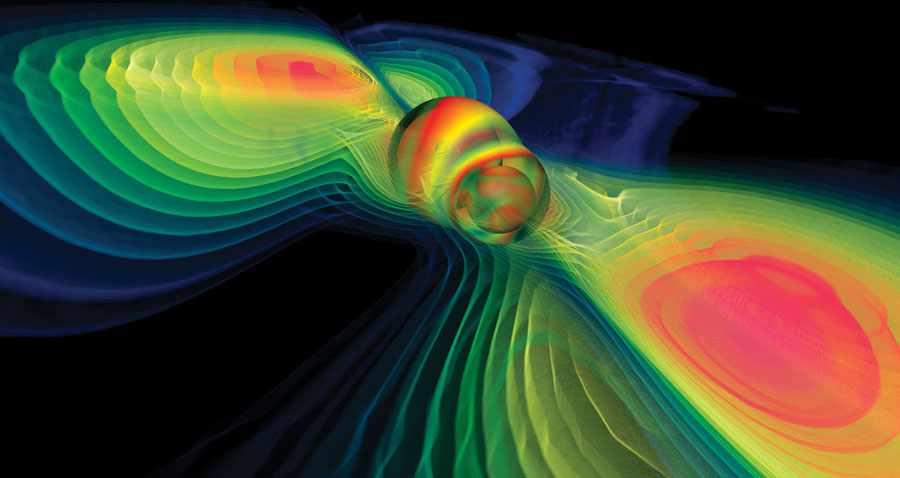
Một mô phỏng của hai lỗ đen đang lướt qua nhau và phát ra sóng hấp dẫn. (Ảnh: Werner Benger/AEI/CCT/ZIB)
Các phương trình Einstein của thuyết tương đối tổng quát trông như dãy núi Hamilaya vậy – đẹp và hùng vĩ khi nhìn từ xa, nhưng lại trơn tuột và đầy kẻ nứt khi tiến đến gần. Trong số những người liều lĩnh làm việc với chúng, không phải ai cũng sống sót mà bước trở ra. Là một tập hợp gồm 10 phương trình vi phân riêng phần phi tuyến, độc lập, các phương trình Einstein liên hệ năng lượng và vật chất trong một vùng không gian với hình học của nó. Thật đơn giản đến bất ngờ khi biểu diễn ở dạng hình học, ngôn ngữ độc lập tọa độ của những tensor mà Einstein cuối cùng đã tìm ra, các phương trình trên – khi áp dụng cho những tình huống thực tế - thật đáng tiếc lại trở nên kết hợp với thứ hoang dại mà không một nhà vật lí nào thuần hóa nổi kể từ thời Newton.
Các phương trình Einstein của thuyết tương đối tổng quát chỉ có thể giải chính xác trong vài ba trường hợp – với một trong những nghiệm đầu tiên như thế, và có lẽ là nghiệm nổi tiếng nhất của nó, được suy luận ra bởi nhà thiên văn học người Đức Karl Schwarzschild vào năm 1916 cho trường hợp đơn giản một vật tĩnh, hình cầu, không tích điện trong chân không. Các giả thuyết của Schwarzschild, và thuật toán của ông, đơn giản các phương trình Einstein đến một phương trình vi phân bình thường mà ông có thể giải dễ dàng, mặc dù ngay cả một bậc thầy như ông cũng cảm thấy bất ngờ trước khả năng có một nghiệm chính xác. “Nghiệm Schwarzschild” một cách tự nhiên đã đưa đến khái niệm lỗ đen, mặc dù bản thân Schwarzschild chưa bao giờ hiểu thấu tầm quan trọng của sự kì dị trong nghiệm của ông, vì ông đã qua đời 4 tháng sau đó ở tiền phương nước Nga trong Thế chiến thứ nhất. Ngay cả Einstein cũng nghĩ điểm kì dị Schwarzschild – bán kính tại đó nghiệm là không hợp lí do chia cho không – là vô nghĩa về phương diện vật lí, và chỉ hàng thập kỉ sau này thì chiều sâu của nghiệm Schwarzschild mới nở hoa trong thời kì vàng son thứ nhất của thuyết tương đối tổng quát, kéo dài từ khoảng năm 1960 đến 1975, với những tên tuổi như Roger Penrose, Kip Thorne, Stephen Hawking và nhiều người khác.
Khi các lí thuyết phát triển, thuyết tương đối tổng quát đã có sự thành công to lớn. Nổi tiếng nhất là những nghiệm gần đúng ban đầu của nó đã giải thích cho một sự chênh lệch đã biết trong quỹ đạo của Thủy tinh mà người ta không thể nào giải thích hoàn toàn bằng vật lí học Newton cổ điển, mang lại một giá trị cho sự chênh lệch đó phù hợp với các phép đo thiên văn. Các phương trình Einstein còn dự đoán rằng ánh sáng bẻ cong trong một trường hấp dẫn và tín hiệu radar bị trễ khi phản xạ khỏi một trong những hành tinh nhóm trong của hệ mặt trời của chúng ta. Tuy nhiên, những thành công này đều dựa trên sự gần đúng “hậu Newton” của những phương trình Einstein đầy đủ, trong đó những tốc độ là nhỏ so với tốc độ ánh sáng và trường hấp dẫn là yếu. Thuyết tương đối tổng quát Einstein chưa bao giờ được kiểm tra trong chế độ “trường mạnh” khác biệt rất nhiều.
Tuy nhiên, nhờ những siêu máy tính nhanh và cực mạnh, ngày nay các nhà vật lí có thể nghiền ngẫm bằng cách thuần hóa lực qua các phương trình Einstein, sử dụng những thuật toán điện toán tiên tiến. Sử dụng cái gọi là “thuyết tương đối số”, chúng ta có thể khảo sát những chế độ vật lí trong đó không-thời gian khác xa với thế giới đơn giản, phẳng, 4D của thuyết tương đối đặc biệt, thu được những nghiệm chính xác ở cả nơi lực hấp dẫn là mạnh và ở cả nơi không gian và thời gian bị kéo dãn hoặc xoắn lại. Thật vậy, các nhà lí thuyết đã có một số đột phá quan trọng trong việc giải các phương trình Einstein trên máy vi tính, dẫn tới những tiên đoán đặc biệt mà các nhà thiên văn ngày nay có thể kiểm tra.
Với sự phân tích và quan sát hội tụ lại, người ta đã thu được những cái nhìn sâu sắc mới về một số hiện tượng ngoạn mục và giàu năng lượng nhất trong vũ trụ, hóa ra đang thúc đẩy các nhà tương đối học số nghiên cứu những hệ ngày một phức tạp hơn, tỏng những chế độ mà các nhà vật lí trước đây chưa bao giờ xâm nhập tới. Những phương pháp này đã làm sáng tỏ khả năng của những lỗ đen “lêu lổng”, bị tống cổ ra khỏi hang ổ thiên hà của chúng để lẳng lặng lao đi trong không gian giữa các sao. Chúng còn trở thành một công cụ để tìm hiểu cơ chế động lực học của các cặp lỗ đen, để khảo sát phương trình trạng thái của sao neutron, và để giúp chúng ta thiết kế ra những máy dò tương lai đặt trên không gian săn tìm sóng hấp dẫn – những dao động nhỏ xíu trong cấu trúc của bản thân không-thời gian. Như được biết, đó chính là thời kì vàng son mới của thuyết tương đối tổng quát.
Tinh vi và hiểm độc
Kể từ thập niên 1960, các nhà tương đối học đã cố gắng giải các phương trình Einstein bằng phương pháp số, nhưng việc rút ra cơ sở vật lí từ thậm chí những trường hợp đơn giản thôi cũng tỏ ra hết sức khó khăn. Ngay từ đầu, các nhà lí thuyết đã thiết lập những phương pháp khéo léo nhằm đóng gói bài toán cho máy vi tính xử lí bằng cách chia không-thời gian 4D thành một chồng mặt 3D được đánh nhãn bằng một thông số thời gian. Nhưng những ai sử dụng cách tiếp cận như thế đều nhận thấy các chương trình máy tính của họ bị phá sản sau khi trở nên mất ổn định và chịu sai số lớn – thậm chí trong những trường hợp đơn giản như hai lỗ đen va chạm trực diện với nhau. Dường như Einstein rốt cuộc cũng chẳng đúng: bài toán ấy vừa tinh vi lẫn hiểm độc.
Bài toán đó lại trở nên cấp thiết hồi thập niên 1990 khi nước Mĩ bắt đầu lên kế hoạch cho Đài thiên văn Sóng hấp dẫn Giao thoa kế Laser (LIGO) – hai giao thoa kế khổng lồ ở Washington và Louisiana cuối cùng bắt đầu thu thập dữ liệu vào năm 2002 trong cuộc truy tìm vẫn đang diễn ra tìm kiếm sóng hấp dẫn. Để trích ra những tín hiệu sóng hấp dẫn nhỏ xíu từ phông nền nhiễu, các nhà thiết kế cần phải biết dạng thức chính xác của sóng hấp dẫn mà người ta hi vọng sẽ lan qua trên thiết bị - nhất là biên độ và tần số của chúng – vì những dao động này sẽ được xác định chính xác bởi những cánh tay của giao thoa kế thay đổi chiều dài của chúng bao nhiêu, và bao nhanh. Nhưng lúc ấy, các nhà lí thuyết đang nghiên cứu các hiện tượng thiên văn vật lí mà người ta trông đợi phát ra những sóng như thế, đặc biệt là hai lỗ đen hợp nhất, chỉ có thể hỗ trợ các nhà thiết kế LIGO với những gợi ý chung chung mà thôi. “Hồi thập niên 1990, các phương trình Einstein cho hai lỗ đen đang va chạm trở thành món chén thánh của thuyết tương đối tổng quát”, Laura Cadonati, một nhà hiện tượng học hấp dẫn tại trường Đại học Massachusetts ở Amherst, nhớ lại. Ông là người đã áp dụng các kết quả số cho các hệ thiên văn vật lí.
Vấn đề thật không đơn giản. Ngoài việc tạo ra sự mất ổn định, các chương trình cuối cùng còn cần phải chạy trong một khoảng thời gian đủ lâu để có được một vài dấu hiệu sau cùng của một cặp lỗ đen quay quanh nhau, sự hợp nhất của chúng và sau đó là sự ổn định của lỗ đen cuối cùng. Các nhà tương đối học đã bị sa lầy: các máy tính của họ, và nhất là phương pháp của họ, có thể xử lí những phần khác nhau của bài toán – trong hai chiều không gian, hoặc chỉ cho đến khi hợp nhất – nhưng không thể xử lí toàn bộ sự kiện có thể xảy ra trong vũ trụ thực tế.

Hình 1. Sóng hấp dẫn phát ra trong sự hợp nhất của hai lỗ đen cùng khối lượng M, theo ước tính của Frans Pretorius ở trường Đại học Princeton, sử dụng các mô phỏng của thuyết tương đối tổng quát. Màu xanh lục là biên độ bằng không, màu tím là dương và màu đỏ là âm. Chuỗi thời gian từ trên xuống dưới, từ trái sang phải ở mỗi hàng. Mỗi ảnh cách nhau thời gian 25 M, còn bề rộng và bề cao của mỗi hộp là khoảng 100 M (tính theo đơn vị trong đó hằng số hấp dẫn và tốc độ ánh sáng đều được đặt bằng 1). Vài khung hình đầu có chứa bức xạ giả mạo đi cùng với dữ liệu ban đầu, chúng nhanh chóng rời khỏi khung hình. Hai lỗ đen cuối cùng hợp nhất để chứa một chân trời sự cố duy nhất tại thời điểm 529 M (hàng thứ năm, thứ hai từ trái sang). (Ảnh: Frans Pretorius)
Sau đó, vào năm 2005, một nghiên cứu sinh hậu tiến sĩ tại Viện Công nghệ California, phần lớn làm việc một mình, đã làm cộng đồng tương đối học bị choáng với một mô phỏng số ổn định của hai lỗ đen khối lượng bằng nhau, ban đầu không quay xung quanh nhau từ quỹ đạo sau cùng, đơn nhất của chúng đến ổn định (hình 1). Frans Pretorius đã thiết lập các phương trình Einstein theo một cách khác với những người khác đang làm, mang lại cho ông những ít phương trình hơn và dễ giải hơn. Kĩ xảo của ông là sử dụng những tọa độ làm cho các phương trình vi phân từng phần mô tả những biến thiên trong không-thời gian giống hệt với phương trình sóng chuẩn mà các nhà vật lí đã biết và đã quen thuộc.
“Một số thứ đã đến cùng lúc với nhau”, Pretorius nhớ lại sự thành công của ông, “trong đó cũng có sự may mắn nữa”. Pretorius cuối cùng mất hai năm cho vấn đề đó. Ông cho biết ông đã nhận được sự hỗ trợ tích cực từ các đồng nghiệp như David Garfinkle và Carsten Gundlach, rất nhiều sự động viên vật chất lẫn tinh thần, và một chương trình siêu máy tính chạy trong hai tháng.
Pretorius, hiện nay làm việc tại trường Đại học Princeton, nhận thấy sự hợp nhất đó mang lại một lỗ đen quay tròn gấp 1,90 lần khối lượng của một trong hai lỗ đen ban đầu. Nó có một xung lượng góc khoảng bằng 0,70 lần bình phương khối lượng lỗ đen sau cùng, và chừng 5% tổng khối lượng ban đầu của nó bị bức xạ dưới dạng sóng hấp dẫn – những con số trước đó chưa có ai tính ra. Pretorius còn tính ra dạng sóng chi tiết của những phát xạ theo một hàm vô hướng đặc trưng cho không-thời gian, cái có thể liên hệ với biên độ biến thiên theo thời gian của một sóng hấp dẫn và, hóa ra, những biến thiên hết sức nhỏ của chiều dài các cánh tay của một máy dò sóng hấp dẫn. Vì chương trình của ông tiếp tục chạy mà không bị phá sản, Pretorius nghĩ “Ôi trời, chương trình này có thể hoạt động nè”, cho đến khi ông trải qua cái ông cho biết là “phần thưởng tức thời với một liều endorphin” khi nó đã cuối cùng hoàn tất. Kết quả của Pretorius, ngày nay gọi là công thức điều hòa khái quát, đã phá vỡ bế tắc của lĩnh vực nghiên cứu.
Vào cuối năm đó, các nhà nghiên cứu tại trường Đại học Texas ở Brownsville và Trung tâm Bay Vũ trụ Goddard của NASA, độc lập nhau, đã phát triển một kĩ thuật khác cho các nghiệm số lỗ đen, gọi là phương pháp “đánh thủng động”, phương pháp nhanh chóng được phần đông cộng đồng chấp nhận vì nó chính xác hơn, ngoại trừ ở chỗ là phức tạp hơn về mặt điện toán. Một vật tương tự thô 2D là mô hình của không-thời gian trong đó hai tấm vải song song nhau, mỗi tấm có một cãi đĩa tại chân trời sự cố của một lỗ đen, được may lại với nhau xung quanh chu vi đĩa. Những sự đáng thủng này – phần bên trong của lỗ đen bị loại khỏi vùng điện toán – sau đó di chuyển khắp mạng lưới biểu diễn không-thời gian khi sự điện toán diễn ra, thể hiện sự chuyển động trong thời gian của chân trời sự cố của lỗ đen.

Hình 2. Mô phỏng của một cặp lỗ đen đang quay tròn có khối lượng bằng nhau. Khi hai lỗ đen quay xung quanh nhau, chúng ảnh hưởng đến plasma xung quanh, gây ra những vòi bức xạ điện từ được cấp năng lượng từ động năng của lỗ đen (màu xanh lục/xanh lam). Trên nguyên tắc, các nhà thiên văn có thể nghiên cứu hệ bằng cách phát hiện bức xạ này – cũng như sóng hấp dẫn phát ra khi hai lỗ đen tương tác. (Ảnh: Luis Lehner, Steven L Liebling, David Neilsen và Carlos Palenzuela).
“Mọi người thích ứng rất nhanh, với cả hai phương pháp”, phát biểu của Luis Lehner thuộc Viện Vật lí Lí thuyết Perimeter ở Waterloo và trường Đại học Guelph, cả hai đều ở Canada. Thách thức hiện nay cho Lehner lẫn những người khác là tìm xem “chúng ta có thể đi tới câu trả lời bao nhanh, và chúng ta có thể tìm kiếm điều không ngờ đó ở đâu để mở rộng kiến thức của chúng ta và làm phát sinh thêm những câu hỏi mới”. Các nhà nghiên cứu tại Goddard sớm tính ra, lần đầu tiên, sự hợp nhất của những lỗ đen khối lượng không bằng nhau, nghiên cứu trong quá trình giật lùi của lỗ đen sau cùng. Kết quả trên được tìm thấy chỉ phụ thuộc vào tỉ số của khối lượng của hai lỗ đen hợp nhất, chứ không phụ thuộc giá trị khối lượng của riêng từng lỗ đen, làm cho dạn sóng hấp dẫn tính được là có thể áp dụng cho nhiều tình huống thiên văn vật lí đa dạng. Tổng năng lượng giải phóng trong quá trình đó – và thời gian cần thiết cho hai lỗ đen hợp nhất – tỉ lệ với tổng khối lượng, nghĩa là sự hợp nhất có thể trong thời gian ngắn tỏa sáng hơn tất cả các ngôi sao trong vũ trụ kết hợp lại.
Những mô phỏng đầu tiên này là thuộc những lỗ đen ban đầu không quay tròn trước khi chúng va chạm, và không bao lâu sau thì một nhóm nghiên cứu tại trường Đại học Texas ở Brownsville đã tiến hành nghiên cứu đầu tiên của sự hợp nhất của những lỗ đen đang quay tròn – với cả hai trường hợp trục quay của chúng thẳng hàng và không thẳng hàng. Thật vậy, những tiến bộ liên tục về kĩ thuật và công suất điện toán đã cho phép các nhà nghiên cứu tính ra cái xảy ra khi những lỗ đen đang quay tròn này va chạm trong nhiều quỹ đạo khác nhau. Các nhà lí thuyết và nhà thực nghiệm bắt đầu hòa hợp, không còn cay cú như chó với mèo nữa, như Cadonati lịch sự nói “để cải thiện tiềm năng của khoa học sóng hấp dẫn và làm thế nào cho phù hợp với thiên văn học vật lí” (hình 2). Các nhà lí thuyết tất bật đưa những con số thực tế vào trong những phương trình đẹp đẽ của họ, còn các nhà thực nghiệm thì cố moi những ghi chép thời nghiên cứu hậu tiến sĩ của họ về phân tích tensor.
Các lỗ đen bị sút văng điVào năm 2007, các nhà tương đối học số đã tìm thấy một sự hợp nhất bất ngờ những mô phỏng của họ. Những xét đoán trực tiếp của cơ chế cơ học của những lỗ đen khối lượng không bằng nhau, đang quay tròn, cho thấy, để bảo toàn xung lượng góc, bức xạ hấp dẫn mà chúng tạo ra sẽ không phát ra đồng đều theo mọi hướng. Hàm ý là lỗ đen sau cùng được tạo ra khi hai vật thể va chạm phải có một xung lượng tuyến tính nào đó so với khối tâm: nói chung, chúng sẽ nhận một “cú sút”. Nhưng những mô phỏng đầy đủ của Manuela Campanelli cùng những đồng sự tại Viện Công nghệ Rochester ở New York, và sau đó là José González cùng các cộng sự tại trường Đại học Jena ở Đức, cho thấy xung lượng này là không nhỏ: lỗ đen cuối cùng có thể có tốc độ lớn tới 4000 km/s đối với hai lỗ đen đang quay tròn theo hướng ngược nhau. (Để so sánh, những ngôi sao ở gần Mặt trời của chúng ta hiếm khi chuyển động đến vài chục km/s).
Gần đây, những tốc độ còn cao hơn, hay “siêu sút”, đã được tìm thấy lên tới 15 000 km/s, với một số nhà lí thuyết đề xuất rằng những tốc độ cao hơn ba lần nữa – hay bằng 15% tốc độ ánh sáng – có lẽ là có thể. Vì những cú sút như thế sẽ lớn hơn vận tốc thoát của bất kì thiên hà nào, nên kết quả trên mở ra khả năng có những lỗ đen cư trú trong những quầng thiên hà ở xa nhân thiên hà của chúng, hay có lẽ còn có những lỗ đen độc lập, lang thang trôi giạt trong vũ trụ. Những lỗ đen này phần lớn sẽ không được nhìn thấy cho đến khi chúng đi lạc vào, nói thí dụ, đám mây Oort của các sao chổi nằm cách Mặt trời khoảng một năm ánh sáng, khi đó người ta có thể phát hiện ra chúng qua những sự lệch bí ẩn, nhỏ xíu trong sự chuyển động của các sao chổi hay tiểu hành tinh. Một sự kiện ít có khả năng xảy ra là một lỗ đen lêu lỏng đi qua hệ mặt trời của chúng ta, nên chúng ta không nên lo lắng về khả năng này.
Kém thê thảm hơn, những cú siêu sút có những gợi ý cho những ai đang tìm kiếm sóng hấp dẫn. Những lỗ đen bị tống vọt ra khỏi những đám sao hình cầu – tập hợp những ngôi sao quay xung quanh nhân thiên hà như một vệ tinh – sẽ làm giảm tốc độ hợp nhất sau đó đối với những lỗ đen còn lại trong đám, và vì thế sẽ làm giảm số lượng sóng hấp dẫn đi tới máy dò sóng. Những cú giật lùi lớn cũng sẽ loại bỏ những lỗ đen vận tốc cao, và có thể ràng buộc những lỗ đen mầm nhỏ sẽ hợp nhất thành lỗ đen lớn hơn bao sớm trong vũ trụ.
Thư Viện Vật Lý
